English

SUDOKU-ANLEITUNG

Diese Anleitung ist eine Übersetzung von Solving Sudoku von Angus Johnson. Er ist auch der Autor von Simple Sudoku, dem bevorzugten Sudoku-Programm der blechtrottel.net.

Für die Unterstützung bei besonders kniffligen Stellen danken wir Jeff Waldock von der Firma Quick Translation in Wien.

Diese Anleitung kann auch als PDF-Datei heruntergeladen werden.

Die einzige Regel

• Füllen Sie die leeren Felder so, dass in jeder Zeile, jeder Spalte und jedem 3x3-Kästchen die Zahlen 1 bis 9 nur einmal vorkommen.

Grundlegendes

Vorab ist zu bemerken, dass man bei der Lösung nicht weit kommen kann, ohne eine gewissenhafte Liste der möglichen Werte oder Kandidaten für ein leeres Feld zu führen. Händisch ist das aufwändig und auch fehleranfällig und oft lenkt es vom eigentlichen Spaß an der Lösung dieser Rätsel ab. Zum Glück erledigen Programme wie Simple Sudoku das für Sie, somit bleibt Ihnen die Freude das Rätsel mit Logik zu lösen.

Falls Sie kein Programm zur Unterstützung haben, so analysieren Sie systematisch jedes leere Feld. Gehen Sie dabei von der Annahme aus, dass es jeden Wert zwischen 1 und 9 annehmen kann, und streichen Sie dann alle Werte, die bereits in anderen Feldern derselben Zeile, Spalte oder des 3x3-Kästchens (im folgenden Gruppe genannt) vorkommen. Auf diese Weise erhalten Sie für jedes leere Feld eine Liste von Kandidaten.

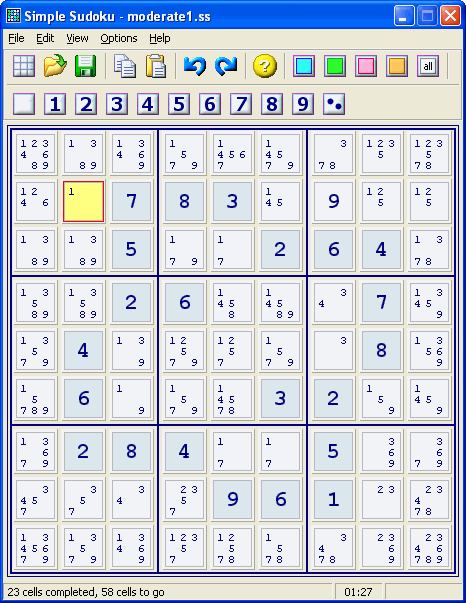
Wiederholen Sie die folgenden logischen Schritte bis das Rätsel gelöst ist. Greifen Sie nur dann zu komplizierteren Methoden, wenn Sie mit einfacheren weder neue Werte ermitteln, noch weitere Kandidaten ausschließen können.

 

Einzelne Kandidaten (Singles)

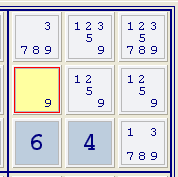Jedem Feld, für das es nur einen Kandidaten gibt, kann dieser Wert zugewiesen werden.

Dabei ist es sehr wichtig, jedesmal, wenn ein Wert in ein Feld eingetragen wird, diesen auch als Kandidaten in allen anderen Feldern in derselben Gruppe zu streichen. (Programme wie Simple Sudoku erledigen auch diese anstrengende Arbeit für Sie.)

 

Versteckte einzelne Kandidaten

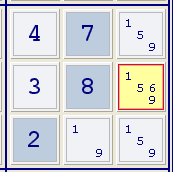Sehr oft gibt es nur einen Kandidaten für eine bestimmte Gruppe, doch versteckt er sich unter anderen.

Im Beispiel rechts findet sich die Zahl 6 nur im mittleren rechten Feld der 3x3-Kästchens. Da die Zahl 6 in jedem Kästchen vorkommen muss, muss das das Feld sein.

Weiterführendes

Die beiden oben angeführten Schritte führen als einzige direkt zu einem Wert; man kann damit nur die einfachsten Rätsel lösen. Das ist gut so, denn sonst wären Sudokus heute nicht so populär. Die folgenden Schritte werden (mit steigendem Schwierigkeitsgrad) die Zahl der Kandidaten in den leeren Feldern so lange verringern helfen, bis früher oder später ein einzelner Kandidat oder versteckter einzelner Kandidat überbleibt.

 

Fixe Kandidaten 1 (Locked Candidates)

Manchmal ist ein Kandidat in einem Kästchen auf eine Zeile oder Spalte beschränkt. Da eines dieser Felder diesen Kandidaten enthalten muss, kann er in den anderen Feldern dieser Zeile oder Spalte gestrichen werden.

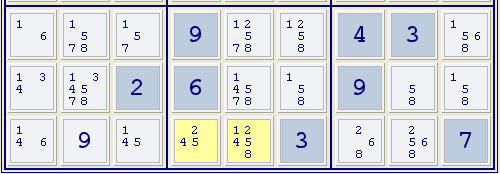
Im nachstehenden Beispiel findet sich im rechten Kästchen die Zahl 2 nur in der untersten Zeile. Da eines dieser Feld die Zahl 2 sein muss, kann sie in keinem Feld in derselben Zeile außerhalb dieses Kästchens vorkommen. Daher kann die Zahl 2 als Kandidat in den markierten Feldern ausgeschlossen werden.

 

Fixe Kandidaten 2 (Locked Candidates)

Manchmal kommt ein Kandidat in einer Zeile oder Spalte nur in einem Kästchen vor. Da eines dieser Felder diesen Kandidaten enthalten muss, kann er aus den übrigen Feldern in diesem Kästchen gestrichen werden.

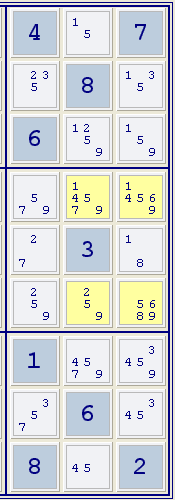
Im Beispiel rechts kann die Zahl 9 für die linke Spalte nur im mittleren Kästchen vorkommen. Da eines dieser Felder die Zahl 9 sein muss (denn sonst gäbe es sie in dieser Spalte nicht), kann sie aus allen Feldern dieses mittleren Kästchens mit Ausnahme der linken Spalte gestrichen werden.

 

Freie Paare (Naked Pairs)

Wenn zwei Felder einer Gruppe ausschließlich ein identisches Kandidatenpaar enthalten, dann können diese beiden Zahlen in keinem anderen Feld dieser Gruppe vorkommen.

Diese beiden Kandidaten können aus den anderen Feldern dieser Gruppe entfernt werden.

Im nachstehenden Beispiel bilden die Kandidaten 6 und 8 in den Spalten 6 und 7 ein freies Paar in dieser Zeile. Daa ja eines dieser Felder die Zahl 6 sein muss und das andere die Zahl 8, können sie daher aus allen anderen Feldern dieser Zeile gestrichen werden (in unserem Fall betrifft das nur das markierte Feld).

Fortgeschrittenes

 

Freie Dreiergruppe & Freie Vierergruppe
(Naked Triples & Naked Quads)

Das gleiche Prinzip wie bei freien Paaren lässt sich auch auf freie Dreiergruppen und freie Vierergruppen anwenden.

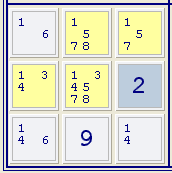
Eine freie Dreiergruppe liegt dann vor, wenn drei Felder in einer Gruppe nur dieselben drei Kandidaten enthalten. Die Felder, die die freie Dreiergruppe bilden, müssen nicht jeden der drei Kandidaten enthalten. Wenn diese Kandidaten in anderen Feldern der Gruppe vorkommen, können sie gelöscht werden.

Im Beispiel rechts bilden im Kästchen die Felder oben links, unten links und unten rechts eine freie Dreiergruppe, denn sie enthalten nur die Kandidaten 1, 4 und 6. Deshalb können die Kandidaten 1 und 4 in den markierten Feldern ausgeschlossen werden.

 

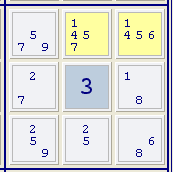Ein freie Vierergruppe kommt vor, wenn vier Felder in einer Gruppe nur dieselben vier Kandidaten enthalten.

Im Beispiel rechts bilden die Kandidaten 2, 5, 7 und 9 in den drei linken Feldern und im mittleren Feld unten eine freie Vierergruppe. Deshalb können die Kandidaten 5 und 7 in den markierten Feldern gelöscht werden.

 

Versteckte Paare (Hidden Pairs)

Enthalten zwei Felder in einer Gruppe ein Kandidatenpaar (versteckt unter anderen), das nicht in einem anderen Feld dieser Gruppe vorkommt, dann können die anderen Kandidaten in diesen zwei Feldern ausgeschlossen werden.

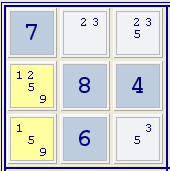
Im Beispiel rechts finden sich die Kandidaten 1 und 9 nur in den beiden markierten Feldern eines Kästchens, und bilden deshalb ein verstecktes Paar. Alle Kandidaten bis auf 1 und 9 können aus diesen beiden Feldern gestrichen werden, da ein Feld die Zahl 1 sein muss, während das andere die Zahl 9 ist.

 

Versteckte Dreiergruppe (Hidden Triples)

Wenn sich drei Kandidaten auf drei Felder in einer bestimmten Gruppe beschränken, dann können alle anderen Kandidaten in diesen drei Feldern gestrichen werden.

Im nachstehenden Beispiel finden sich die Kandidaten 3, 6 und 7 nur in den Spalten 4, 6 und 7. Deshalb können alle anderen Kandidaten aus diesen drei Feldern entfernt werden.

Versteckte Dreiergruppen sind extrem schwer zu erkennen. Zum Lösen eines Rätsels braucht man sie allerdings nur selten.

 

Versteckte Vierergruppe (Hidden Quads)

Wenn vier Kandidaten sich auf vier Felder in einer Gruppe beschränken, dann können alle anderen Kandidaten in diesen vier Feldern ausgeschlossen werden.

Versteckte Vierergruppen sind sehr selten. Sie sind fast nicht zu erkennen, selbst wenn man weiß, dass es eine geben muss.

Versuchen Sie, die versteckte Vierergruppe in der nachstehenden Zeile zu entdecken.
(Bewegen Sie den Mauszeiger über das Bild, um die Lösung zu sehen.)

Für Spezialisten

Die folgenden Techniken sind nicht komplizierter als die oben angeführten, doch muss man dafür erkennen, wie bestimmte Kandidaten (in bestimmten Mustern) über jegliche Zeile, Spalte oder jegliches Kästchen hinaus zueinander in Beziehung stehen.

»X-Wing«

In jedem Sudoku kann ein Wert nur einmal in jeder Zeile, Spalte oder einem Kästchen vorkommen. Wenn ein Wert in einer bestimmten Zeile nur an zwei Stellen vorkommen kann (d.h. er ist nur in zwei Feldern dieser Zeile Kandidat), dann muss er in einem dieser beiden Felder vorkommen. Nehmen wir einmal an, in einem Rätsel ist in zwei Zeilen ein Kandidat C auf genau dieselben zwei Spalten beschränkt. Da aber

1. Kandidat C in jeder der zwei Zeilen genau einmal vorkommen muss, und
2. keine Spalte mehr als einen der Kandidaten enthalten darf,

muss Kandidat C genau einmal in jeder dieser zwei Spalten in diesen beiden Zeilen vorkommen. Daher kann kein anderes Feld in diesen beiden Spalten den Kandidaten C enthalten. Dieselbe Logik gilt auch für ein Rätsel, bei dem in zwei Spalten der Kandidat C auf genau zwei Zeilen beschränkt ist.

Im nachstehenden Beispiel wird dies verdeutlicht. Ein Filter wurde angewandt, sodass nur die Kandidaten für die Zahl 6 zu sehen sind. (Felder, die den Kandidaten enthalten, werden in Simple Sudoku automatisch hellgrün markiert, sofern sie nicht noch umgefärbt werden - wie z.B. das blaue Feld in diesem Beispiel.)

Die blau gekennzeichneten Felder bilden einen »X-Wing«, da die Zeilen 1 und 9 beide nur zwei Felder mit dem Kandidaten 6 aufweisen und diese zwei Felder in den gleichen zwei Spalten liegen. Daher kann man die anderen Kandidaten für die Zahl 6 in den Spalten 6 und 9 (gelb gekennzeichnet) entfernen.

(Anmerkung: Kandidat C muss entweder 1. oben links und unten rechts vorkommen, oder 2. unten links und oben rechts in den Ecken des Rechtecks, das von diesen beiden Zeilen und Spalten gebildet wird. Das Muster, das die sich schneidenden Diagonalen bilden, ist wahrscheinlich der Ursprung des Namens dieser Technik.)

 

»Swordfish«

Das »Swordfish« (Schwertfisch)-Muster ist eine Variante des »X-Wing«-Musters von oben.

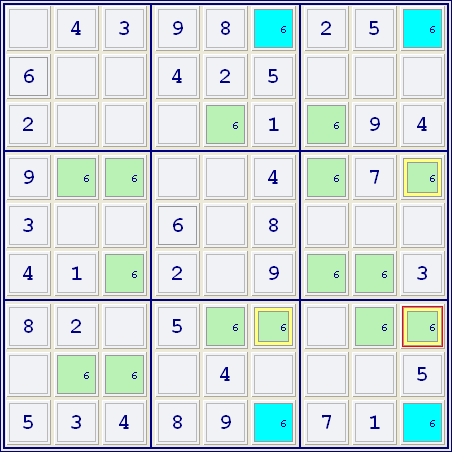
Im nachstehenden Beispiel zeigt ein Filter nur die Kandidaten für die Zahl 5.

Drei Zeilen (3, 5 und 7) haben einen Kandidaten in höchstens drei Feldern (nur jeweils zwei Felder in diesem Beispiel) und diese Felder teilen sich alle dieselben drei Spalten (3, 4 und 7). Ein Swordfish-Muster ist gegeben. Andere Kandidaten für die Zahl 5 in diesen drei Spalten (gelbe Markierung) können ausgeschlossen werden.

Anmerkung: Wie aus diesem Beispiel ersichtlich ist, müssen es nicht genau drei Felder in jeder Zeile (oder Spalte) sein, es können auch weniger sein. Jedoch können es nicht mehr als drei Kandidaten in den das Muster definierenden Zeilen sein.

Wer besonders aufmerksam ist, kann auch den inversen »Swordfish« im obigen Beispiel erkennen (der dieselben Kandidaten ausschließt). Es ist aber nicht wichtig, welchen »Swordfish« Sie zuerst entdecken ...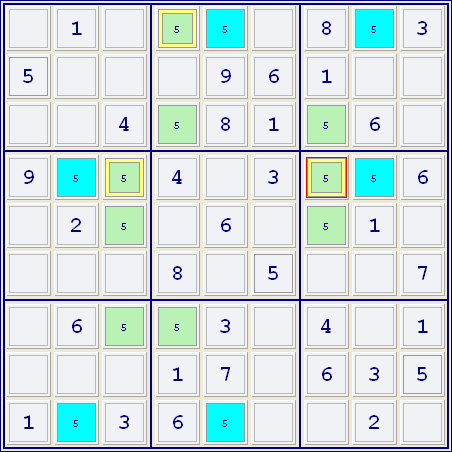

Noch immer verwirrt? Klicken Sie hier für weiterführende Informationen zum Thema »Swordfish« (auf englisch).

Die »X-Wing«- und »Swordfish«-Technik kann auf Zeilen erweitert werden, in denen Kandidaten auf vier Felder in denselben vier Spalten beschränkt sind (dies wird »Jellyfish« (Qualle) genannt).    

Lösung durch Farbzuweisung

Uns interessieren dabei einzelne Kandidaten, die nur in zwei Feldern einer Gruppe vorkommen. Diese beiden Felder sind miteinander verbunden, denn eines muss den Wert enthalten (wahr sein), während das andere ihn nicht enthalten darf (also falsch sein muss). Da wir noch nicht wissen, was auf welches Feld zutrifft, besteht die allgemein üblich Strategie darin, diese Beziehung durch zwei verschieden Farben anzuzeigen (in unserem Fall wurden willkürlich Blau und Grün für die nachfolgenden Beispiele gewählt). Üblicherweise gibt es zu jedem Zeitpunkt eine Reihe von verbundenen Paaren. Manchmal sind diese mit anderen verknüpft und bilden eine Kette sich abwechselnder wahrer und falscher Feldwerte. Diese Ketten können Kandidaten aufzeigen, die ausgeschlossen werden können.

Immer, wenn zwei Felder in einer solchen Kette dieselbe Farbe haben und zu ein und derselben Gruppe gehören, muss diese Farbe falsch sein, denn in jeder Gruppe darf jeder Wert ja nur einmal vorkommen.

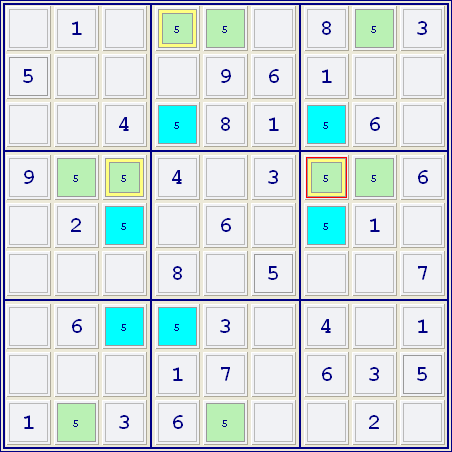
Im folgenden Beispiel wurde bis auf die Zahl 9 alle Kandidaten herausgefiltert. (Felder, in denen der gefilterte Kandidat vorkommt, werden von Simple Sudoku automatisch hellgrün markiert, sofern sie danach nicht umgefärbt werden - was außer einem alle Felder dieses Beispiels betrifft). Man kann unschwer erkennen, dass es eine Reihe verbundener Paare gibt, die man in einer Kette abwechselnd färben kann. Vom Feld Z2S2 ausgehend, das hier willkürlich grün gefärbt ist, trifft man auf zwei verbundene - das Feld Z6S2 (da es nur zwei Kandidaten 9 in Spalte 2 gibt) und Feld Z2S3 (weil es in Zeile 2 nur zwei Kandidaten 9 gibt), die blau gefärbt sind. Zu beiden blauen Felder (Z6S2 und Z2S3) gehören andere verbundene Felder, die wieder grün gefärbt sind. Wiederholt man diesen Vorgang durch das Raster, so stellt sich heraus, dass es blaue Felder gibt, die in derselben Gruppe liegen. Da in jeder Gruppe ein Wert nur einmal vorkommen darf, müssen die blauen Felder die falschen Werte darstellen, somit kann man allen hellgrünen Feldern den Wert 9 zuweisen.

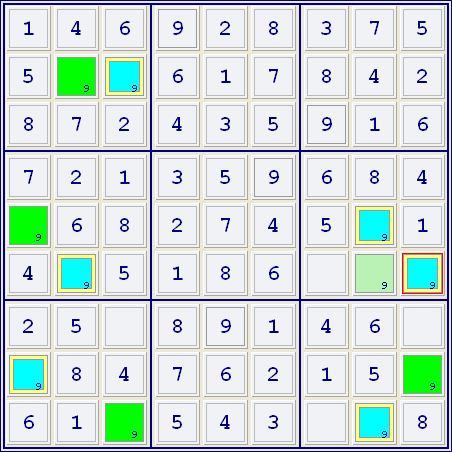
Weiters kann ein Kandidat, der nicht zur Kette gehört und mit zwei verschiedenfarbigen Feldern einer solchen Kette in einer Gruppe steht, ausgeschlossen werden.

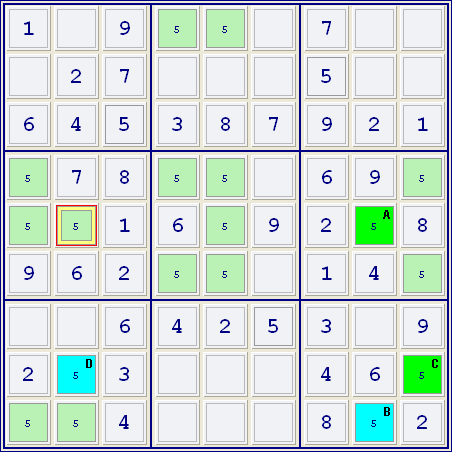
Das kann am besten anhand des nachfolgenden Beispiels gezeigt werden. Ein Filter zeigt nur die Kandidaten der Zahl 5. Feld A und B bilden ein verbundenes Paar, weil sich darin die einzigen Kandidaten für die Zahl 5 in Spalte 8 finden. Die Felder B und C bilden ebenfalls ein solches Paar, weil sie die einzigen Kandidaten für die Zahl 5 im Kästchen unten rechts sind. Zuletzt bilden Feld C und D ein verbundenes Paar, weil sie als einzige in Zeile 8 den Kandidaten enthalten. Da diese drei Paare alle über andere Beziehungen verbunden sind, bilden sie eine Kette und können wie gezeigt abwechselnd blau und grün gefärbt werden. Das gelb markierte Feld steht mit zusammenhängenden verbundenen Paaren verschiedener Farbe in Beziehung (Feld A und D). Da eine der beiden Farben für den richtigen Wert 5 steht, kann hier dieser Kandidat ausgeschlossen werden.

Mehrfache Farbzuweisung

Es gibt zwei Typen der mehrfachen Farbzuweisung. Filtert man alle bis auf einen bestimmten Kandidaten heraus und erhält so zwei verschiedene verbundene Ketten (Blau & Grün und Rosa & Orange) so gilt:

Typ 1: Gehören blaue Felder zur selben Gruppe wie rosa und orange Felder, dann muss der Kandidat in den blauen Feldern falsch sein, weil ja entweder der in den rosa oder der in den orange Feldern richtig ist.

Beispiel für Typ 1:

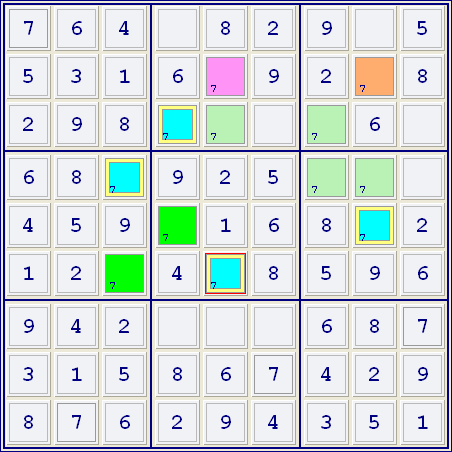
Filtert man alles außer der Zahl 7 heraus und die blauen und hellgrünen Felder sind verbundene Paare, wie auch das rosa und das orange Feld, so muss der Kandidat in den blauen Feldern falsch sein, da ja entweder das rosa oder das orange Feld richtig ist und die blauen Felder mit beiden zu einer Gruppe gehören. Der Kandidat 7 kann aus allen blauen Feldern gestrichen werden.

Typ 2: Stehen blaue Felder in derselben Gruppe wie das orange Feld, dann kann aus jedem Feld mit diesem Kandidaten, das sowohl mit den grünen Feldern als auch mit dem rosa Feld in eine Gruppe gehört, der Kandidat gelöscht werden. Begründung: Die Kandidaten in den blauen Feldern und dem orange Feld können nicht beide richtig sein, also muss entweder eines der grünen Felder oder das rosa Feld richtig sein oder beide. Deshalb kann aus jedem Feld, das sowohl mit einem grünen und dem rosa Feld in einer Gruppe liegt, der Kandidat gelöscht werden.

Beispiel für Typ 2:

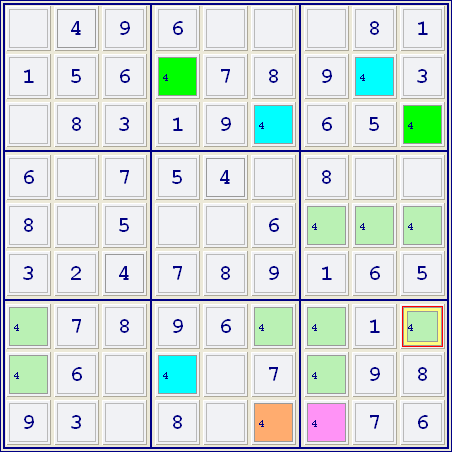
Hier wurden Kandidaten für die Zahl 4 stehen gelassen. Die blauen und hellgrünen Felder sind verbunden wie auch das rosa und das orange Feld - also können das orange und die blauen Felder nicht beide richtig sein, da sie zur selben Gruppe gehören. Deshalb sind entweder das rosa Feld oder die hellgrünen Felder richtig und folglich kann für jedes Feld in derselben Gruppe mit einem rosa und einem hellgrünen (also Z7S9) der Kandidat 4 gelöscht werden.

»XY-Wing«

Nicht zu verwechseln mit dem »X-Wing« (siehe oben).

Begründung: Wenn man einem Feld, das zur selben Gruppe gehört wie beide Ast-Felder, den Kandidaten z zuweist, dann kann dieser in keinem Zweig stehen. In der Folge wäre ein Zweig x und der andere y und somit der Stamm ohne Kandidat, was unmöglich ist.

Anmerkung: Wenn alle drei Felder in einem »XY-Wing«-Muster zur selben Gruppe gehören, dann bilden sie eine freie Dreiergruppe.

Beispiel:

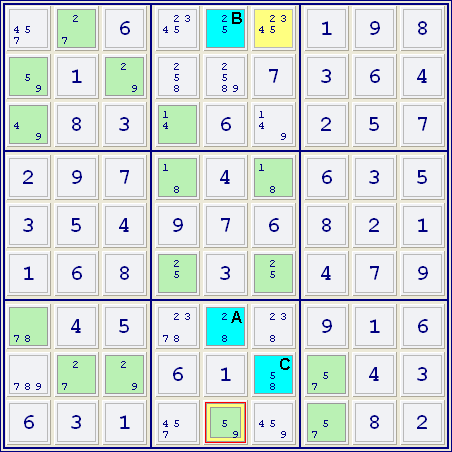
Das Feld Z7S5 (A) ist der Stamm und Z1S5 (B) und Z8S6 (C) sind die Äste, die den Kandidaten 5 in beiden Ästen aufweisen. Daher kann aus jedem Feld, das zu einer Gruppe mit beiden Ästen gehört, der Kandidat 5 gelöscht werden (d.h. aus Z1S6 und Z9S5).

Schließlich gibt es noch Lösungstechniken (z.B. »Forcing Chains«), die den Umfang dieser Webseite sprengen würden. Manche Sudokus lassen sich mit einfacher Logik nicht lösen und können nur durch Ausprobieren gelöst werden. Es gibt auch Rätsel, die mehrere Lösungen haben; sie werden im allgemeinen als ungültig und fehlerhaft angesehen.